Radiologia Brasileira - Publicação Científica Oficial do Colégio Brasileiro de Radiologia

Endereço para correspondência

 

>

 

INTRODUÇÃO

A simulação do comportamento da radiação ionizante em determinado meio pode ser realizada mediante conhecimento dos vários processos físicos de interação^(1,2). Neste estudo biológico, partículas são transportadas ao longo de materiais análogos aos do corpo do ser humano, sendo o processo do cálculo de dose dividido em duas fases: a primeira independe da geometria do meio absorvedor e refere-se à simulação da produção do feixe de radiação pelo acelerador linear e da geração dos espaços de fase, onde podem ser encontradas informações sobre a energia e posição das partículas; na segunda fase, as partículas que constituem o espaço de fase são transportadas através da geometria considerada, codificada a partir da informação contida em imagens obtidas por uma tomografia axial computadorizada e da distribuição de dose absorvida^(3,4).

O PENELOPE, algoritmo que usa o método de Monte Carlo, é um código computacional utilizado para simulações diversas^(3,5). Este algoritmo é baseado no modelo de espalhamento que combina uma base numérica de dados com modelos de seção de choque para os diferentes mecanismos de interação, sendo aplicável a energias (energia cinética no caso de elétrons e pósitrons) de algumas centenas de eV a aproximadamente 1 GeV. A simulação de fótons é feita por intermédio do método convencional de forma detalhada, enquanto a de elétrons e pósitrons é feita por um processo misto^(3,4). Uma característica importante deste código é que a parte mais delicada desta simulação é tratada internamente; assim, elétrons, pósitrons e fótons são simulados utilizando a mesma sub-rotina. Do ponto de vista do usuário, PENELOPE permite que a simulação de elétrons e pósitrons seja tratada de forma tão simples quanto a de fótons, embora a simulação de partículas carregadas exija maior tempo de processamento^(3-6).

Este código tem sido usado com muita frequência, caracterizando-se como ferramenta muito útil para simulações com geometrias complexas, como no caso de heterogeneidades^(7-9). O código PENELOPE descreve ainda, com precisão, o transporte de fótons e elétrons na matéria e alcança bons resultados na vizinhança das interfaces entre materiais⁽⁷⁾. Mesmo com alto nível de exatidão, o tempo gasto para se obter os resultados da simulação ainda é grande; por isso, seu uso na prática clínica ainda é limitado. Sua maior utilidade está na comparação de dados experimentais com dados obtidos pelo sistema de planejamento.

É importante demonstrar que as simulações obtidas com o uso do código PENE-LOPE mostram resultados semelhantes aos obtidos experimentalmente, de modo a futuramente poder ser utilizado mais amplamente nos sistemas de planejamento dos serviços de radioterapia.

O principal objetivo deste trabalho, ao utilizar o algoritmo PENELOPE com o método de Monte Carlo e desenvolver geometrias onde estão presentes heterogeneidades, é simular o espaço percorrido pelo feixe de fótons gerado pelo sistema nessas geometrias. Assim, são obtidas curvas que mostram a variação da dose absorvida com a profundidade, e as perturbações causadas pelas heterogeneidades.

 

MATERIAIS E MÉTODOS

Foram feitas simulações para o caso homogêneo, ou seja, o simulador contendo somente água, e para o caso heterogêneo, em que foram introduzidas heterogeneidades que variaram, principalmente, em termos da densidade do material.

Durante toda essa etapa foi utilizado computador com processador Intel^® Core T 2 Quad, CPU Q6600, 2.40 GHz, 2 GB de memória RAM. Os programas foram escritos utilizando GNU Fortran g77.

Geometria dos fantomas

A geometria do fantoma é cúbica, com lados iguais a 40 cm e as heterogeneidades com a forma de paralelepípedos de dimensões 40 x 40 x 10 cm³. Para simular as heterogeneidades de maior importância para a clínica, foram introduzidos os seguintes materiais no fantoma: tecido simulador de osso e de pulmão, de acordo com a International Commission on Radiological Protection, titânio (material utilizado em próteses metálicas), alumínio (eventual substituto do osso) e prata (principal componente de amálgamas).

Simulação em Monte Carlo

A simulação realizada com o subprograma PENEASY do PENELOPE pode ser feita em uma única etapa ou mais etapas. No presente estudo, foi feita em apenas uma etapa, pois se tratava de uma fonte monoenergética.

Foram definidos, como parâmetros de entrada⁽¹⁰⁾: a energia e o tipo de partícula da fonte, 6 MV de fótons; a distância fonte-superfície, 100 cm; e o campo de tratamento, 10 x 10 cm².

Ainda no arquivo de entrada foram definidas as propriedades dos materiais dos fantomas: energia de absorção de elétrons e pósitrons, em todos os materiais, 100 keV, ou seja, elétrons e pósitrons com energia cinética inferior a 100 keV serão absorvidos pelo meio; energia de absorção de fótons, em todos os materiais, 10 keV, ou seja, fótons com energia inferior a esta serão absorvidos pelo meio; energia de corte para colisões inelásticas, 10 keV, ou seja, somente perdas de energia superiores a este valor serão consideradas; energia de corte para emissões bremsstrahlung, 1 keV, ou seja, somente fótons emitidos com energia superior a esta serão considerados.

A trajetória do feixe de fótons é simulada no fantoma e repetida para cada fantoma, para que sejam obtidas e comparadas as curvas de dose absorvida em função da profundidade para cada material introduzido separadamente.

Durante a simulação foi gerado um arquivo, o tallySpatialDoseDistrib.dat, com informações sobre a distribuição espacial de dose. Para se obter dados sobre a dose absorvida na profundidade Z, modificou-se o arquivo de entrada sobre essa seção de maneira a variar a dose somente no eixo Z, mantendo X e Y constantes. Variou-se a profundidade de 0 a 40,0 cm, pois o fantoma tem 40 cm de profundidade, com um número de bins igual a 100. Este número indica que o intervalo entre as medidas deve ser de 0,4 cm.

 

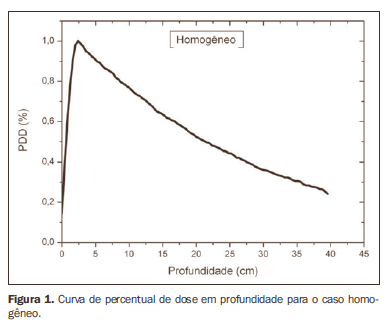
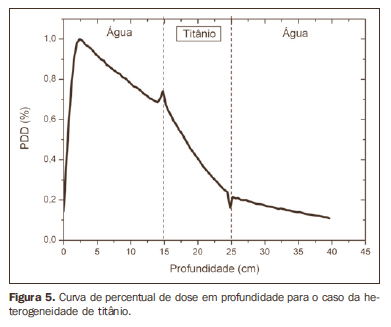
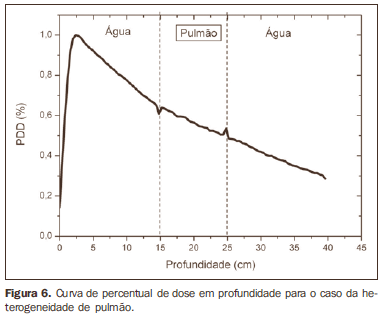
RESULTADOS

A Figura 1 mostra a curva de percentage depth dose (PDD) obtida para o caso homogêneo, apenas água. Os resultados obtidos para as simulações nos casos heterogêneos são apresentados nas Figuras de 2 a 5. As curvas mostram o percentual da dose absorvida em função da profundidade em centímetros.

 

 

 

 

 

 

 

 

 

 

 

 

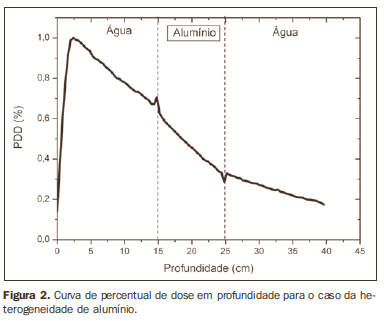
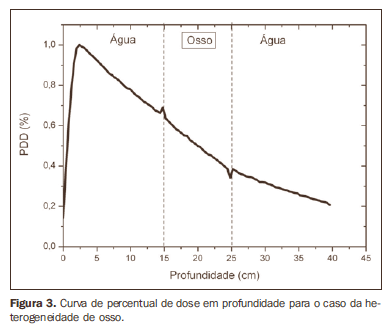
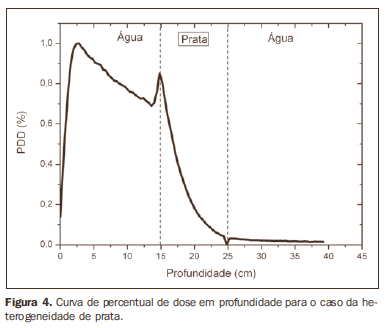
A curva obtida para o caso homogêneo (Figura 1) apresenta tissue phantom ratio (TPR)20,10 = 0,6818, correspondente a um feixe de 6,39 MV. Essa diferença ocorre, pois a simulação foi feita com uma fonte monoenergética de 6 MV, e não com o espectro de um acelerador clínico.

A Figura 2 mostra o comportamento do feixe ao ser introduzida a heterogeneidade de alumínio. Para a profundidade de 24 cm, a dose absorvida no alumínio é 24,2% menor em relação ao fantoma homogêneo. No caso da heterogeneidade de osso (Figura 3), a dose absorvida é 11,1% menor, para a mesma profundidade. A Figura 4 mostra a heterogeneidade de prata, material com alta densidade eletrônica, em que a dose absorvida na profundidade de 24 cm é 89,2% menor que na água; comportamento semelhante pode ser visto na Figura 5, com a heterogeneidade de titânio, material com densidade eletrônica elevada, em que, para a mesma profundidade, a dose absorvida é 44,2% em relação à água. O caso do pulmão (Figura 6) apresenta comportamento diferente dos demais, pois a densidade eletrônica deste material é inferior à da água, assim, a dose absorvida na profundidade de 24 cm é 12,6% maior que a da água.

Nas Figuras de 2 a 5 observa-se uma região de transição onde o espalhamento contribui para um pico na região entre 14,8 e 15,0 cm, início da heterogeneidade, e uma região de perda de build-up entre 24,8 e 25,0 cm, final da heterogeneidade. O pico ocorre quando o feixe passa de um meio de menor densidade para um meio com maior densidade, e a região de perda de build-up ocorre no sentido inverso, de maior densidade para menor densidade. Nos materiais mais densos, como o titânio e a prata, estas regiões tornam-se mais evidentes do que em materiais menos densos, como o osso e o alumínio. A Figura 6, referente à heterogeneidade de pulmão, mostra comportamento oposto da região de espalhamento, ou seja, a região de perda de buildup fica na região entre 14,8 e 15,0 cm, e a região de build-up, na região entre 24,8 e 25,0 cm, pois a densidade do pulmão é menor que a da água. Essas regiões de espalhamento podem contribuir para um aumento desnecessário da dose nos órgãos adjacentes às heterogeneidades.

 

DISCUSSÃO

Neste trabalho foi avaliada a dose absorvida no interior e nas proximidades de alguns materiais contendo heterogeneidades com diferentes densidades, por meio da simulação com o método de Monte Carlo. Quando o paciente é tratado com não homogeneidades contidas em seu corpo, a dose heterogeneidade-tecido pode sofrer alterações. O sucesso ou falha de um tratamento por radiação depende da dose liberada no volume inteiro do tumor e não deve variar mais do que 5% da dose prescrita⁽¹¹⁾. Entre os clínicos existe consenso que, enquanto a superdosagem pode aumentar o risco de necrose, a subdosagem pode comprometer a destruição do tumor e também deve ser avaliada⁽¹²⁾.

O principal objetivo da simulação era verificar o comportamento do feixe de fótons ao passar por interfaces e meios não equivalentes à água. Para analisar o comportamento do feixe, foram obtidas curvas do percentual de dose absorvida em função da profundidade nos fantomas.

Analisando-se as curvas obtidas da dose absorvida em função da profundidade encontra-se, para o caso homogêneo, o TPR20,10 = 0,682, que corresponde a um feixe de 6,4 MV. Essa diferença ocorre, pois a simulação foi feita considerando uma fonte monoenergética de 6 MV, e não com o espectro real de um acelerador. Estudos realizados por Allal et al.⁽¹³⁾ avaliaram a influência das placas de reconstrução facial confeccionadas em titânio sobre as variações da dose na interface metal/tecido, usando um acelerador de 6 MV de fótons. Os resultados mostraram uma sobredosagem na interface titânio/tecido.

Os resultados encontrados no presente trabalho, para os casos heterogêneos, mostram que a dose absorvida independe do número atômico do material, mas varia com o número de elétrons por centímetro cúbico (e/cm³) destes, pois na faixa de energia utilizada, de 6,0 MV, o efeito Compton é predominante^(1,9). Estudos feitos por Carolan et al.⁽¹⁴⁾ avaliaram a influência da presença de próteses coxofemorais na distribuição da radiação em pacientes submetidos a radioterapia, com 6 MV de fótons. Nesse estudo, foram analisadas próteses fundidas a partir de liga Co-Cr-Mo, por possuírem alta densidade eletrônica, apresentando maior impacto na distribuição da dose irradiada. Os resultados mostraram que pode ser visto um aumento da dose no tecido acima da prótese, distante 5 mm, e uma diminuição na dose absorvida no tecido logo abaixo da prótese, quando ela está presente.

A prata, entre os materiais analisados neste trabalho, é o que possui maior densidade eletrônica, de 27,45 x 10²³ e/cm³, enquanto a água tem 3,34 x 10²³ e/cm³ e o pulmão, com menor densidade eletrônica, tem 0,69 x 10²³ e/cm³. Nota-se que em materiais com elevado número de e/cm³, como a prata, a dose absorvida é maior; em contrapartida, no tecido simulador de pulmão, ela é menor. Para a profundidade de 24 cm, por exemplo, a dose absorvida pela prata foi de 89,2% em relação à dose absorvida no fantoma homogêneo.

Pode-se também observar, nas curvas de PDD, que o espalhamento no início e no final das heterogeneidades corresponde a uma região de pico e uma região de perda de build-up. Essas regiões ficam mais evidentes em materiais mais densos, como a prata. Gez et al.⁽¹⁵⁾ avaliaram a perturbação na dose devido à presença de um stent prostático (50% Ni e 50% Ti) em pacientes recebendo radioterapia pélvica, com feixe de 6 MV de fótons. Os resultados mostraram aumento de 20% na dose imediatamente acima do stent e diminuição de 18% abaixo dele. O aumento na dosagem foi atribuído ao espalhamento de elétrons provocado pelo stent metálico com elevado número atômico, sendo a radiação atenuada pelo stent e não pelo tecido.

 

CONCLUSÃO

Os resultados obtidos neste trabalho demonstram a importância dos algoritmos de cálculo usados nos sistemas de planejamento considerarem heterogeneidades ao calcular a distribuição de dose nos pacientes, evitando subdosagem ou sobredosagem em tecidos próximos⁽¹⁰⁾. Deve-se considerar também a contribuição do espalhamento nas interfaces entre meios com números atômicos muito diferentes, como no caso de próteses metálicas^(10,16-18).

 

REFERÊNCIAS

1. Attix FH. Introduction to radiological physics and radiation dosimetry. 2nd ed. USA: John Wiley & Sons; 1986.         [  ]

2. Khan FM. The physics of radiation therapy. 3rd ed. Philadelphia: Lippincott Williams & Wilkins; 2003.         [  ]

3. Sempau J, Wilderman SJ, Bielajew AF. DPM, a fast, accurate Monte Carlo code optimized for photon and electron radiotherapy treatment planning dose calculations. Phys Med Biol. 2000;45: 2263-91.         [  ]

4. Sempau J, Sánchez-Reyes A, Salvat F, et al. Monte Carlo simulation of electron beams from an accelerator head using PENELOPE. Phys Med Biol. 2001;46:1163-86.         [  ]

5. Verhaegen F, Seuntjens J. Monte Carlo modelling of external radiotherapy photon beams. Phys Med Biol. 2003;48:R107-64.         [  ]

6. Andreo P. Monte Carlo techniques in medical radiation physics. Phys Med Biol. 1991;36:861-920.         [  ]

7. Blazy L, Baltes D, Bordy JM, et al. Comparison of PENELOPE Monte Carlo dose calculations with Fricke dosimeter and ionization chamber measurements in heterogeneous phantoms (18 MeV electron and 12 MV photon beams). Phys Med Biol. 2006;51:5951-65.         [  ]

8. Knöös T, Wieslander E, Cozzi L, et al. Comparison of dose calculation algorithms for treatment planning in external photon beam therapy for clinical situations. Phys Med Biol. 2006;51: 5785-807.         [  ]

9. Jones AO, Das IJ, Jones FL Jr. A Monte Carlo study of IMRT beamlets in inhomogeneous media. Med Phys. 2003;30:296-300.         [  ]

10. Aljarrah K, Sharp GC, Neicu T, et al. Determination of the initial beam parameters in Monte Carlo linac simulation. Med Phys. 2006;33:850-8.         [  ]

11. Souza CN, Monti CR, Sibata CH. Recomendações para se evitar grandes erros de dose em tratamentos radioterapêuticos. Radiol Bras. 2001; 34:29-37.         [  ]

12. Niroomand-Rad A, Razavi R, Thobejane S, et al. Radiation dose perturbation at tissue-titanium dental interfaces in head and neck cancer patients. Int J Radiat Oncol Biol Phys. 1996;34:475-80.         [  ]

13. Allal AS, Richter M, Russo M, et al. Dose variation at bone/titanium interfaces using titanium hollow screw osseointegrating reconstruction plates. Int J Radiat Oncol Biol Phys. 1998;40: 215-9.         [  ]

14. Carolan M, Dao P, Fox C, et al. Effect of hip prostheses on radiotherapy dose. Australas Radiol. 2000;44:290-5.         [  ]

15. Gez E, Cederbaum M, Yachia D, et al. Dose perturbation due to the presence of a prostatic urethral stent in patients receiving pelvic radiotherapy: an in vitro study. Med Dosim. 1997;22: 117-20.         [  ]

16. Ahnesjö A, Aspradakis MM. Dose calculations for external photon beams in radiotherapy. Phys Med Biol. 1999;44:R99-155.         [  ]

17. Deng J, Ma CM, Hai J, et al. Commissioning 6 MV photon beams of a stereotactic radiosurgery system for Monte Carlo treatment planning. Med Phys. 2003;30:3124-34.         [  ]

18. Gibbs FA, Palos B, Goffinet DR. The metal/tissue interface effect in irradiation of the oral cavity. Radiology. 1976;119:705-7.         [  ]

 

 

Endereço para correspondência:
Camila Salata
Rua São Francisco Xavier, 524, Pavilhão Haroldo Lisboa da Cunha, Sala 136, Térreo, Maracanã
Rio de Janeiro, RJ, Brasil, 20550-900
E-mail: camilasalata@bol.com.br

Recebido para publicação em 11/12/2008.
Aceito, após revisão, em 18/6/2009.

 

 

Suporte financeiro: Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes) e Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).
* Trabalho realizado no Laboratório de Ciências Radiológicas do Departamento de Biofísica e Biometria da Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, RJ, Brasil.