Radiologia Brasileira - Publicação Científica Oficial do Colégio Brasileiro de Radiologia

^IMaster, Physicist at Laboratory of Radiological Sciences, Department of Biophysics and Biometry - Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, RJ, Brazil
^IIPhD, Full Professor, Brody School of Medicine, East Carolina University (ECU), Greenville, NC, USA
^IIIPhD, Professor, Department of Nuclear Engineering - Instituto Militar de Engenharia (IME), Rio de Janeiro, RJ, Brazil
^IVPhD, Full Professor, Laboratory of Radiological Sciences, Department of Biophysics and Biometry - Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, RJ, Brazil

Mailing address

INTRODUCTION

The simulation of ionizing radiation behavior in a certain medium can be made provided that the various physical interaction processes are known^(1,2). In this biological study, particles are transported along materials that are analogous to the human body, with the dose calculation process being divided into two phases: the first one is independent from the absorbing medium geometry, and is related to the production of the radiation beam by the linear accelerator and generation of the phase spaces, where information on energy and particles position can be found; in the second phase, the particles constituting the phase space are transported thru the considered geometry, codified on the basis of the information contained in images acquired by an axial computed tomography and absorbed dose distribution^(3,4).

The PENELOPE, an algorithm that uses the Monte Carlo method, is a computational code utilized for several simulations^(3,5). This algorithm is based on the scattering model which combines a numerical data base with shock section models for the different interaction mechanisms, being applicable to energies (kinetic energy in the case of electrons and positrons) from a few hundreds eV to approximately 1 GeV. The photons simulation is performed by means of the conventional method in detailed form, while the electrons and positrons simulation is performed by a mixed process^(3,4). An important characteristic of this code is that the most sensitive part of this simulation is internally treated, thus electrons, positrons and photons are simulated utilizing the same subroutine. From the user's point of view, PENELOPE allows the electrons and positrons simulation to be treated as simply as the photons simulation, although the charged particles simulation requires a longer processing time^(3-6).

This code has been very frequently utilized and has proved to be a valuable tool for simulations with complex geometries as in the case of heterogeneities^(7-9). The PENELOPE code also describes with precision the photons and electrons transportation in the matter and achieves good results in the vicinity of interfaces between different materials⁽⁷⁾. In spite of the high level of accuracy, the time necessary to achieve the simulations results is still long; for that reason its use in the clinical practice is still limited. Its greatest usefulness is in the comparison of experimental data with those obtained by the planning system.

It is important to demonstrate that the simulations obtained with the use of PENELOPE show results similar to those experimentally obtained, thus allowing its future wider utilization in planning systems at radiotherapy centers.

The main purpose of the present study in using the PENELOPE algorithm with the Monte Carlo method and developing geometries in which heterogeneities are present, is to simulate the photon beam path generated by the system in these geometries. Thus, curves showing the variation of absorbed dose with depth and disturbances caused by heterogeneities are obtained.

MATERIALS AND METHODS

Simulations were made for the homogeneous case, that is, with the simulator containing only water, and for the heterogeneous case, in which heterogeneities that varied mainly in terms of material density, were introduced.

Throughout this phase a computer equipped with an Intel^® Core T 2 Quad microprocessor, CPU Q6600, 2.40 GHz, 2 GB RAM memory. The programs were written with the GNU Fortran g77 compiler.

Phantom geometry

The phantom geometry is cubic with 40 cm edges and the heterogeneities are parallelepiped-shaped, measuring 40 × 40 × 10 cm³. In order to simulate heterogeneities of greatest clinical relevance, the following materials were introduced in the phantom: bone and lung tissues simulator, in compliance with the International Commission on Radiological Protection recommendations, titanium (material utilized in metallic prostheses), aluminum (eventual bone substitute) and silver (the main component of amalgams).

Monte Carlo simulation

The simulation performed with the subroutine PENEASY of PENELOPE can be performed in one or more steps. In the present study, the simulation was developed in only one step, considering that the source was monoenergetic.

The following input parameters were defined⁽¹⁰⁾: the energy and type of source particle, 6 MV photons; the source-surface distance, 100 cm; and treatment field, 10 × 10 cm².

Also in the input file, the phantom materials properties were defined: electrons and positrons energy absorption, in all the materials, 100 keV, i.e., electrons and positrons with kinetic energy < 100 keV will be absorbed by the medium; photons absorption energy, in all the materials, 10 keV, with photons with values lower than this energy being absorbed by the medium; cutoff energy for inelastic collisions, 10 keV, i.e., only energy losses higher than this value will be considered; cut-off energy for bremsstrahlung emissions, 1 keV, that is, only photons emitted with values higher than this energy will be considered.

The trajectory of the photon beam is simulated in the phantom, and repeated for each phantom, so that absorbed dose curves as a function of the depth of each material separately introduced can be obtained and compared.

The file tallySpatialDoseDistrib.dat with data on the spatial dose distribution was generated during the simulation. In order to obtain data on the absorbed dose at the Z depth, the input file on this section was modified so that the dose only on the Z axis could be varied, while keeping X and Y constant. The depth ranged from 0 to 40.0 cm, as the phantom is 40 cm deep, with 100 bins. This number indicates that the interval between measurements must be 0.4 cm.

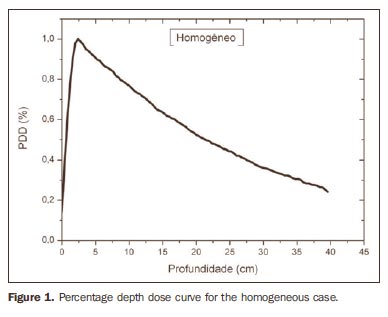
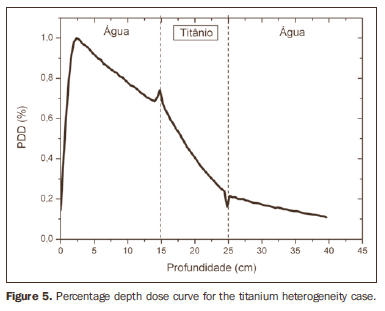
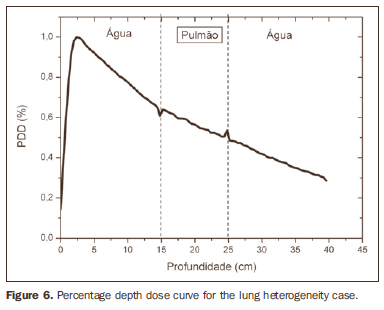
RESULTS

Figure 1 shows the percentage depth dose (PDD) curve obtained for the homogeneous case (only water). The results obtained in the heterogeneous cases are shown on Figures 2 thru 5. The curves show the percentage of absorbed dose as a function of depth in centimeters.

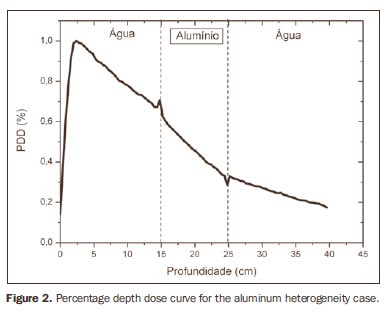
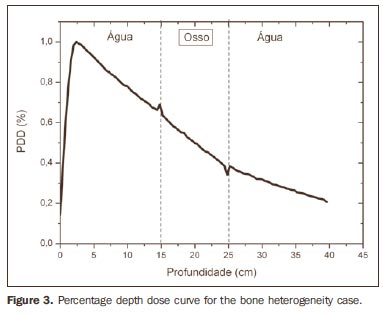
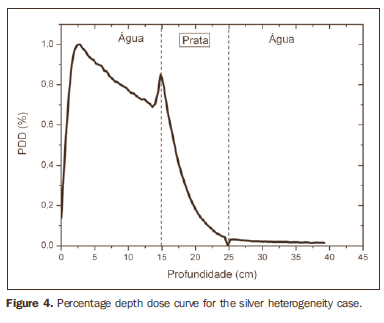
The curve obtained for the homogeneous case (Figure 1) presents a tissue phantom ratio (TPR)20,10 = 0.6818, corresponding to a 6.39 MV beam. This difference is observed because the simulation was made with a monoenergetic source of 6 MV, and not with the spectrum of a clinical accelerator.

Figure 2 shows the behavior of the beam when the heterogeneity of aluminum is introduced. For a depth of 24 cm, the absorbed dose in aluminum is 24.2% lower when compared with the homogeneous phantom.

In the case of bone heterogeneity (Figure 3), the absorbed dose is 11.1% lower for the same depth.

Figure 4 shows the silver heterogeneity, a material with high electronic density, in which the absorbed dose at the 24 cm depth is 89.2% lower than in water; a similar behavior can be seen on Figure 5, with the titanium heterogeneity, a material with high electronic density, in which, at the same depth the absorbed dose is 44.2% in relation to water.

The case of the lung (Figure 6) presents a different behavior from all the others, as the electronic density of this material is lower than that of water. Thus, in this case the absorbed dose at the 24 cm depth is 12.6% higher than that of water.

On Figures 2 thru 5, a transition region can be observed, where the scattering contributes for a peak in the region between 14.8 and 15.0 cm, where heterogeneity begins, and a region of build-up loss, between 24.8 and 25.0 cm, the end of the heterogeneity. The peak occurs when the beam passes from a lower density medium to a higher density medium, and the buildup loss region occurs in the reverse sense, from higher to lower density. In denser materials, such as titanium and silver, these regions become more evident than in less dense materials, such as bone and aluminum. Figure 6, related lung heterogeneity, shows opposite behavior in the scattering region, that is, the build-up loss region is between 14.8 and 15.0 cm, and the buildup region is between 24.8 and 25.0 cm, since the lung density is lower than that of water. These scattering regions may contribute for an unnecessary dose increase in organs adjacent to heterogeneities.

DISCUSSION

In the present study the absorbed dose was evaluated in the interior and in the proximity of certain materials containing heterogeneities with different densities by means of Monte Carlos simulations. When a patient is treated with non-homogeneities in his/her body, the heterogeneity-tissue dose may undergo alterations. The success or failure of a radiation therapy depends on the dose delivered to the whole volume of the tumor, and shall not vary by more than 5% of the prescribed dose⁽¹¹⁾. There is a consensus amongst practitioners that an overdose may increase the risk for necrosis, and an underdose may impair the destruction of the tumor, and should also be evaluated⁽¹²⁾.

The main objective of the simulation was to study the behavior of the photon beam as it passes through interfaces and media not equivalent to water. In order to evaluate the behavior of the beam, curves of absorbed dose percentages as a function of depth in the phantoms, were obtained.

Analyzing the obtained absorbed dose curves as a function of depth, one finds the TPR20,10 = 0.682, for the homogeneous case, which corresponds to a 6.4 MV beam. This difference is observed because the simulation was performed considering a monoenergetic source of 6 MV, and not the actual spectrum of an accelerator. Studies developed by Allal et al.⁽¹³⁾have evaluated the influence of facial reconstruction plates made from titanium on the dose variations in the metal/tissue interface, utilizing a 6 MV photons accelerator. The results demonstrated an overdose in the titanium/tissue interface.

The results of the present study, for the heterogeneous cases, show that the absorbed dose does not depend on the atomic number of the material, but varies with the number of electrons by cubic centimeter (e/cm³) of the material because, in the energy range of 6.0 MV utilized, the Compton effect is predominant^(1,9). Studies developed by Carolan et al.⁽¹⁴⁾ have evaluated the influence of the presence of coxofemoral prostheses on the radiation distribution in patients submitted to radiotherapy with 6 MV of photons. In this study, prostheses cast with Co-Cr-Mo alloys were analyzed due to their high electronic density, presenting greater impact on the irradiated dose distribution. The results have demonstrated that an increase in dose can be observed in the tissue above the prosthesis, at 5 mm, and a decrease in absorbed dose in the tissue immediately below the prosthesis, when it is present.

Silver, amongst the materials analyzed in the present study, is the one with the highest electronic density, 27.45 × 10²³ e/cm³, while water has 3.34 × 10²³ e/cm³ and the lung, with lower electronic density, has 0.69 × 10²³ e/cm³. It is observed that, in materials with a high number of e/cm³, such as silver, the absorbed dose is higher; on the other hand, in the lung tissue simulator, it is lower. For the depth of 24 cm, for example, the absorbed dose by silver was 89.2% in relation to the dose absorbed in the homogeneous phantom.

In the PDD curves, one can also observe that the scattering in the beginning and at the end of heterogeneities corresponds, respectively, to a peak region and a region of build-up loss. These regions are more evident in denser materials such as silver. Gez et al.⁽¹⁵⁾ have evaluated the dose disturbance due to the presence of a prostatic stent (50% Ni and 50% Ti) in patients undergoing pelvic radiotherapy, with 6 MV photon beams. The results demonstrated a 20% dose increase immediately above the stent and 18 % reduction below it. The increase in dose was attributed to electron scattering caused by the metal stent with a high atomic number, with the radiation being attenuated by the stent and not by the tissue.

CONCLUSION

The results obtained in the present study demonstrate the importance of taking the heterogeneity into consideration in the calculation algorithms utilized in planning systems when calculating dose distribution in patients, avoiding underdose or overdose in adjacent tissues⁽¹⁰⁾. The scattering contribution in interfaces between media with very different atomic numbers should also be taken into consideration, like in the case of metal prosthesis^(10,16-18).

REFERENCES

1. Attix FH. Introduction to radiological physics and radiation dosimetry. 2nd ed. USA: John Wiley & Sons; 1986.         [  ]

2. Khan FM. The physics of radiation therapy. 3rd ed. Philadelphia: Lippincott Williams & Wilkins; 2003.         [  ]

3. Sempau J, Wilderman SJ, Bielajew AF. DPM, a fast, accurate Monte Carlo code optimized for photon and electron radiotherapy treatment planning dose calculations. Phys Med Biol. 2000;45: 2263-91.         [  ]

4. Sempau J, Sánchez-Reyes A, Salvat F, et al. Monte Carlo simulation of electron beams from an accelerator head using PENELOPE. Phys Med Biol. 2001;46:1163-86.         [  ]

5. Verhaegen F, Seuntjens J. Monte Carlo modelling of external radiotherapy photon beams. Phys Med Biol. 2003;48:R107-64.         [  ]

6. Andreo P. Monte Carlo techniques in medical radiation physics. Phys Med Biol. 1991;36:861-920.         [  ]

7. Blazy L, Baltes D, Bordy JM, et al. Comparison of PENELOPE Monte Carlo dose calculations with Fricke dosimeter and ionization chamber measurements in heterogeneous phantoms (18 MeV electron and 12 MV photon beams). Phys Med Biol. 2006;51:5951-65.         [  ]

8. Knöös T, Wieslander E, Cozzi L, et al. Comparison of dose calculation algorithms for treatment planning in external photon beam therapy for clinical situations. Phys Med Biol. 2006;51: 5785-807.         [  ]

9. Jones AO, Das IJ, Jones FL Jr. A Monte Carlo study of IMRT beamlets in inhomogeneous media. Med Phys. 2003;30:296-300.         [  ]

10. Aljarrah K, Sharp GC, Neicu T, et al. Determination of the initial beam parameters in Monte Carlo linac simulation. Med Phys. 2006;33:850-8.         [  ]

11. Souza CN, Monti CR, Sibata CH. Recomendações para se evitar grandes erros de dose em tratamentos radioterapêuticos. Radiol Bras. 2001; 34:29-37.         [  ]

12. Niroomand-Rad A, Razavi R, Thobejane S, et al. Radiation dose perturbation at tissue-titanium dental interfaces in head and neck cancer patients. Int J Radiat Oncol Biol Phys. 1996;34:475-80.         [  ]

13. Allal AS, Richter M, Russo M, et al. Dose variation at bone/titanium interfaces using titanium hollow screw osseointegrating reconstruction plates. Int J Radiat Oncol Biol Phys. 1998;40: 215-9.         [  ]

14. Carolan M, Dao P, Fox C, et al. Effect of hip prostheses on radiotherapy dose. Australas Radiol. 2000;44:290-5.         [  ]

15. Gez E, Cederbaum M, Yachia D, et al. Dose perturbation due to the presence of a prostatic urethral stent in patients receiving pelvic radiotherapy: an in vitro study. Med Dosim. 1997;22: 117-20.         [  ]

16. Ahnesjö A, Aspradakis MM. Dose calculations for external photon beams in radiotherapy. Phys Med Biol. 1999;44:R99-155.         [  ]

17. Deng J, Ma CM, Hai J, et al. Commissioning 6 MV photon beams of a stereotactic radiosurgery system for Monte Carlo treatment planning. Med Phys. 2003;30:3124-34.         [  ]

18. Gibbs FA, Palos B, Goffinet DR. The metal/tissue interface effect in irradiation of the oral cavity. Radiology. 1976;119:705-7.         [  ]

Mailing address:
Camila Salata
Rua São Francisco Xavier, 524, Pavilhão Haroldo Lisboa da Cunha, Sala 136, Térreo, Maracanã
Rio de Janeiro, RJ, Brasil, 20550-900
E-mail: camilasalata@bol.com.br

Received December 11, 2008.
Accepted after revision June 18, 2009.

* Study developed at Laboratory of Radiological Sciences, Department of Biophysics and Biometry - Universidade do Estado do Rio de Janeiro (UERJ), Rio de Janeiro, RJ, Brazil. Financial support: Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (Capes) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).