Radiologia Brasileira - Publicação Científica Oficial do Colégio Brasileiro de Radiologia
AMB - Associação Médica Brasileira CNA - Comissão Nacional de Acreditação
 Vol. 44 nº 6 - Nov. / Dec. of 2011
Vol. 44 nº 6 - Nov. / Dec. of 2011
|
ORIGINAL ARTICLE
|
|
Simulation and dosimetric analysis of proton and carbon ion therapy in the treatment of uveal melanoma |
|
|
Autho(rs): Marília Tavares Christóvão1;Tarcisio Passos Ribeiro de Campos2;Bruno Machado Trindade3 |
|
|
Keywords: Carbon ion therapy; Proton therapy; Geant4; Siscodes. |
|
|
Abstract: INTRODUCTION
The treatment of uveal melanoma—the primary ocular tumor with the highest in cidence—, has undergone significant changes over time, with increasing introduction of modalities that allow preservation of the eyeball, as local resection, brachytherapy and external radiotherapy. The utilization of proton and carbon ion in external radiotherapy is advantageous as it provides a spatial form of ionizing energy deposition that is predominant at the end of the pathway of incident particles, represented by a curve whose maximum amplitude is known as Bragg peak(1). The depth of occurrence of Bragg peak depends on the initial energy of incident particle; thus, the site of maximum deposition of ionizing energy is controlled by the initial velocity of the incident particle. As a consequence, healthy tissues located anteriorly and posteriorly to the Bragg peak can be preserved, while increasing the dose delivered to the target tissue, thus obtaining a higher rate of tumor control through the variation of physical parameters applied in the therapy. In carbon ion therapy, the beams are generally applied in a narrow format called pencil beam. The absorbed energy is deposited over the whole target through multiple pencil beams of particles with incident energy covering a wide spectrum, with lower lateral and scattered radiation as compared with proton beams. However, carbon ions present ionization after the Bragg peak, exposing regions immediately posterior to the peak to doses corresponding to 10% to 20% of the value at the Bragg peak(1). Carbon ion therapy is indicated in cases of T2 and T3 lesions(2) located at a distance < 3 mm from the optic disk and for proton and photon-resistant tumors(3), as described on Table 1. 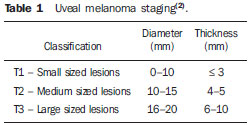 A high radiation dose accurately applied in association with the high linear energy transfer (LET) of the carbon ion beam enhances the tumor control, an essential factor to achieve satisfactory treatment outcomes( 4,5). The objective of the present article is the dosimetric evaluation of radiotherapy with carbon ion and proton pencil beams in ocular tumors. Results from computer simulations based on the Geant4 (GEometry ANd Tracking) code utilized for simulation of particle transport in matter, will be presented. MATERIALS AND METHODS Computational environment and software tools Based on the model of a typical hadrontherapy facility defined at the Geant4, modules were developed and integrated with the purpose of simulating the radiotherapy environment utilizing carbon ion beams. The defined target was an eye model discretized into voxels originated from the Visible Man Project (VMP)(6), adapted and imported into the Siscodes (Computer System for Dosimetry in Radiotherapy)( 7) by Mourão & Campos(8) and implemented in the Monte Carlo N-Particle transport code system (MCNP) version 5. The Siscodes is a computational system designed for three-dimensional planning and simulation of radiotherapy, running as an interface for MCNP, which utilizes stochastic methods for the evaluation of de posited dose(7). The three-dimensional model ocular region was utilized to generate depth dose profiles and isodose curves.In the voxel model of the ocular region, the main structures such as the ocular bulb, muscles and optic nerve were represented. Such non-isotropic model comprised 82 × 100 × 43 voxels, corresponding to a volume of 41 × 50 × 38.7 mm3, representing a matrix whose volume element measured 0.5 × 0.5 × 0.9 mm3(8). Water was the material adopted for each voxel where the carbon ions and protons transport occurred; but the isodoses were plotted superimposed over the material present in the eye phantom. Considering the detailing of the proton therapy study based on such computational environment, dosimetric evaluations dedicated to proton therapy were published(9). In the present study, for the purpose of comparisons between different therapeutic modalities, the simulations utilizing carbon ion and proton beams were performed with the same tools, model and computational environment. Simulation parameters The beam particle release system utilized in the simulations was the passive type, according to the parameters defined in the Geant4 hadrontherapy application.The passive system relies on devices along the irradiation line to produce a homogeneous dose field and to degrade and modulate the beam energy(10). Thus, for simulations with protons beam the passive system was utilized, where the beam entrance position is at the beginning irradiation line, comprising all line elements, the modulation system was not activated. The beams range and applied dose are defined by physical parameters of the utilized components, such as absorbing material and collimators, with the proton kinetic energy being defined at 62 MeV. The parameters regarding the thickness of absorbing material constituted of polymethylmethacrylate (PMMA), applied in the degradation of the proton beams were 6.0 and 8.0 mm. The beam can move along the X and Y coordinates, changing the position of the Bragg peak within the eyeball, simulating the irradiation in different regions of the target.In clinical applications, the target volume dimensions should be taken into consideration in the collimator configuration. For the simulations with carbon ion beams, the ion source position is at 30 cm from the target, utilizing only the final collimator, with a diameter of 5.0 mm, as a part of the passive system. The beam range is defined by the employed energy and the beam was moved, changing the site of the dose deposition to simulate the irradiation in different regions of the target. For ions, the specific energy of the incident particles is defined as the ratio between total energy and the atomic mass number (MeV.amu–1 or MeV.u–1)(11). The number of incident particles utilized for the simulations with proton beam is 100 times greater than that the number for the carbon ion beam, following the values presented in the hadrontherapy facility( 12,13). A synchrotron accelerates protons up to 250 MeV and carbon ions up to 430 MeV/u, with extraction of up to 1011 protons per second and 109 ions per second(12,13). In order to calculate the applied carbon ion current, one must consider the carbon ions charge. On its turn, the total kinetic energy of the ions was obtained by multiplying the energy/mass unit by the carbon-12 mass. In heavy ion radiotherapy planning, a pencil beam is defined and its displacement is defined according to the target position and dimensions, considering the preservation of sensitive structures such as the optic nerve, the lacrimal gland and the crystalline. The simulations for proton and carbon ion beams dosimetry followed a pencil beam protocol without modulation. Depth absorbed dose and dose rate spatial profiles In radiation therapy, the evaluation of dose distribution in target volume is essential in order to assure that the dose deposition is limited to the target, preserving adjacent healthy tissues. The eye model implemented in the Siscodes was utilized to generate the depth dose profiles and the isodose curves(7). The results from the simulations with the Geant4 were translated in Siscodes as depth dose distribution surfaces, superimposed to the ocular voxel model. The simulation output files record data on the energydeposited on the X, Y, and Z voxel coordinates in the AIDA format for generation of distribution graphs and histograms, and in ASCII format. The output file of the simulation in ASCII at the Geant4 is treated by means of a specific in house developed code which converts the code’s output file into the Siscodes format, in MCNP, and calculates the deposited dose rate on each voxel by means of the ratio between the deposited energy in MeV and the specific mass of each voxel, converted into Gy/p units. Such value is adjusted by the RBE factor, resulting in GyE/p (grays equivalent per incident particle). The dose unit recommended for carbon ion and proton radiotherapy is GyE, calculated by multiplying the physical dose expressed in Gy by the RBE, considering the value 3 for carbon ion radiotherapy and 1.1 for proton therapy, following recommendations included in clinical trials(1,3,4,14). Also, the total absorbed dose rate is multiplied by the RBE for carbon ion or proton, whose result is unit of incident particle( 4,15). The dose released by the carbon ion beam is deposited on a geometry in voxel of material and format defined, which is then converted into the Siscodes. The clinical dose adopted for carbon ion is the dose applied in cases of uveal melanoma, 70 GyE, in five sessions(3,4). For the treatment of uveal melanoma with protons, the total dose applied is about 60 GyE released in four fractions of 15 GyE(14). RESULTS Simulations with proton beam In the simulations performed without modulation, with processing of 1.0 × 104 carbon ions, the range and applied current were highlighted. The carbon ion beam energies ranged from 62 to 90 MeV/u. The ranges in the target volume were 11.0 to 21.5 mm, respectively. For each particle kinetic energy applied, simulations were performed with beam displacements, radially in 5.0 mm at right and 7.0 mm at left from the center of the eye lens in the voxel model. The main results obtained in the simulations with carbon ion beam (see Table 2) were the maximum dose (MD) produced per unit of incident particle and the number of incident carbon ions and applied current (nA) required to achieve the dose of 14 GyE, corresponding to one session in the treatment of ocular melanomas. It is possible to observe that the beam current required to achieve 14 GyE presents nonlinear variation with the total energy of the incident proton, in the range of 1.14 to 1.53 nA. The lowest current, 1.14 nA × 10–4, occurs for 840 MeV of carbon-12. 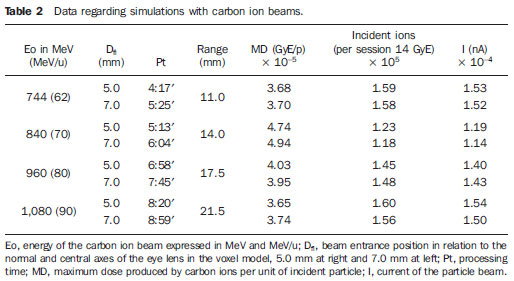 The Bragg peak for carbon-12 beams was well defined. As an example, a typical Bragg peak was reproduced on Figure 1. It was generated without beam modulation, by the pencil beam with a final collimator diameter of 5 mm and displacement of 7.0 mm at left of the center of the eye lens in the voxel model, with incidences of 1.0 × 104 carbon ions and energy of 1,080 MeV or 90 MeV/u. In such a case, the maximum deposited dose was 3.74 GyE/p, in a processing time corresponding to 8 hours and 59 minutes. The range of the Bragg peak was 21.5 mm, as presented on the X axis expressed in voxels with a volume of 0.5 mm3. 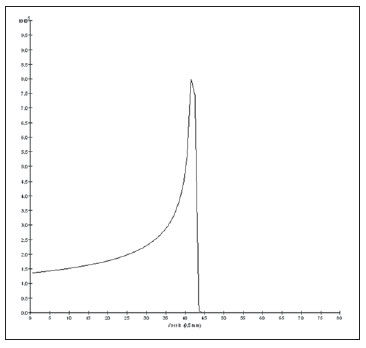 Figure 1. Bragg peak profile related to the energy of 1,080 MeV (90 MeV/u) of the carbon ion beam, represented by deposited energy in eV (× 105) versus multiples of the depth of the number of voxels in 0.5 mm. Similarly to the Bragg peaks, the spatial dose distributions in the simulation on the ocular model are well defined, with low lateral scattering. Figures 2 and 3 present such spatial dose distributions generated at Siscodes, with incidences of 1.0 × 104 carbon ions, and energies of 840 MeV (70 MeV/u) and 960 MeV (80 MeV/u), respectively. 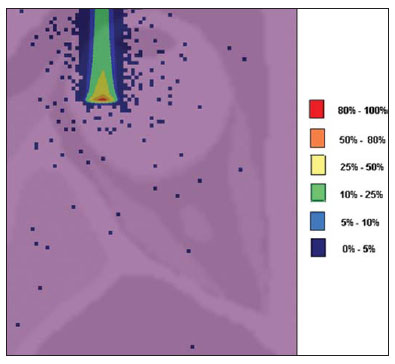 Figure 2. Isodose curve superimposed on the eye model, generated in the Siscodes, corresponding to the simulation performed with carbon ion beam energy of 840 MeV (70 MeV/u) and beam displacement of 7.0 mm at left from eye lens center in the voxel model. 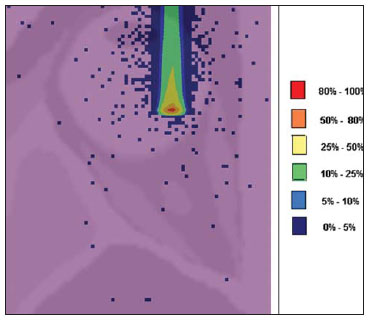 Figure 3. Isodose curve superimposed on the eye model, generated in the Siscodes, corresponding to the simulation performed with carbon ion beam energy of 960 MeV (80 MeV/u) and beam displacement of 5.0 mm at right from eye lens center in the voxel model. In the cases presented on Figures 2 and 3, the maximum deposited doses were 4.94 and 4.03 GyE/p. The dose rates were normalized as a function of the maximum dose for beam entrance in position, incident particle energy and incident carbon ions number.The processing times were 6 hours and 4 minutes and 6 hours and 58 minutes, respectively. Simulations with proton beam The simulations performed without modulation, processing 1.0 × 106 protons, were comparatively performed with the carbon simulations. For such simulations, all devices in the irradiation line were included( 10,14), with the distance covered by the proton beam up to the target corresponding to 2.70 m. The collimator diameter of 5.0 mm and energy of 62 MeV were maintained for all the simulations. The beam range achieved 23.0 and 20.5 mm respectively for application of 6.0 and 8.0 mm of absorbing material. The main results obtained are presented on Table 3 as follows: maximum dose (MD) produced/unit of incident particle, number of incident protons and applied current (nA) required to achieve the dose of 15 GyE, corresponding to one session in the treatment of ocular melanoma by proton therapy. A current of 3.91 to 5.54 nA can be observed in this case. The number of incident protons required to achieve the dose of 15 GyE at the maximum range positions was 3.05 to 4.12 × 1010. 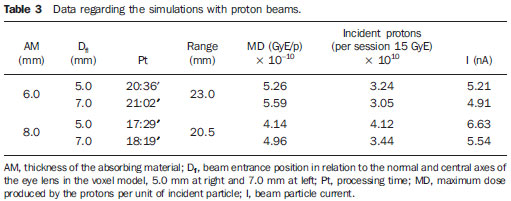 The spatial dose distributions on the eye model were also reproduced. The simulations were performed with proton beam with energy of 62 MeV, with an incidence of 1.00 × 106 protons. In the reproduced cases, displacement of the proton beam entrance position was observed. Polymethylmethacrylate was the absorbing material utilized. The maximum deposited doses were 4.14 and 5.59 GyE/p at the maximum points, as shown on Figures 4 and 5 respectively. The dose rates were normalized as a function of maximum dose for beam entrance in position, incident particle energy and incident carbon ions number. The processing times corresponded to 17 hours and 29 minutes and 21 hours and 2 minutes. 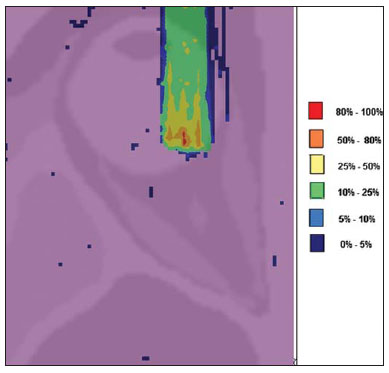 Figure 4. Isodose curve superimposed on the eye model, generated in the Siscodes, corresponding to the simulation performed without modulation of the 62 MeV proton beam, final collimator diameter of 5.0 mm and 8.0 mm of absorbing material. Beam displacement of 5.0 mm at right from eye lens center. 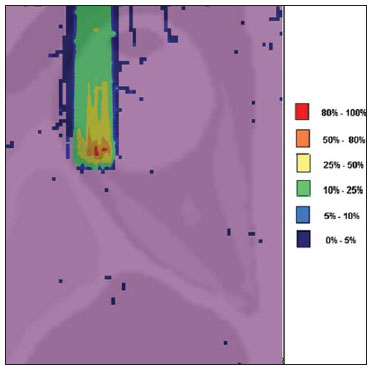 Figura 5. Distribuição espacial de isodoses superposta ao modelo de olho, gerada no Siscodes, referente à simulação executada sem modulação do feixe de prótons de 62 MeV e diâmetro colimador final de 5,0 mm. Deslocamento do feixe de 7,0 mm à esquerda e 6,0 mm de material absorvedor. The Bragg peak in the 62 MeV proton beam simulation with incidence of 1.00 × 106 protons without modulation, was reproduced. In such a case, a collimator with final diameter of 5.0 mm and 6.00 mm of absorbing material were applied, with at left of the center of eye lens in the voxel model. Figure 6 illustrates such peak. Such a simulation resulted in a maximum deposited dose of 5.59 GyE/p. The Bragg peak range was 23.0 mm, present in 0.5 mm3 voxels. A wider peak is observed as compared with the Bragg peak for carbon ion beam, as shown on Figure 1. 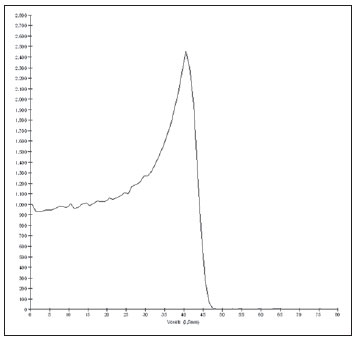 Figura 6. Perfil do pico de Bragg referente à energia 62 MeV do feixe de prótons sem modulação, representado pela energia depositada em eV versus múltiplos da profundidade do número de voxel em 0,5 mm. DISCUSSION The irradiation process and dosimetric parameters applied in the simulations of carbon ion or proton therapy are compatible with those reported in the literature(1– 4,14). The intensities of the incident beams and carbon ions currents were defined so that the clinical dose for the treatment of uveal melanoma (70 GyE – five sessions of 14 GyE) is achieved. In the studies developed by Koyama-Ho et al.(3) and Tsuji et al.(4) of the Research Center Hospital for Charged Particle Therapy, National Institute of Radiological Sciences (NIRS), Chiba, Japan, patients with uveal melanoma were submitted to carbon ion therapy, with doses of 60, 70, 77 and 85 GyE in five fractions, according to tumor size, visual acuity and distance from the optic disc(3,4). These authors have investigated the carbon ion therapy and utilized an incident kinetic energy of 140 MeV/u, considering the complete configuration of the passive beam delivery system, which comprises, among other components, a modulation system and absorbing materials for modulation and degradation of the beam energy. In the present study, energies of 744 MeV (62 MeV/u) to 1,080 MeV (90 MeV/u) were utilized, lower than the energy of 140 MeV/u, based on the characteristics of the computational configurations of the eye model(8) and of the irradiation line(10), where the devices for ion beam modulation and degradation were not activated because of limitations of the distance between the carbon ion source and the target. The beam intensity and carbon ion current applied in the present simulation were comparable to those applied at the NIRS, in order to achieve an equivalent clinical dose for the treatment of uveal melanoma (60 GyE – four sessions of 15 GyE)(14). In a study developed at Centro di Adro-Terapia e Applicazioni Nucleari Avanzate, in Italy, Cirrone et al.(14) have reported the treatment of ocular tumors with proton therapy. A total of 47 patients presenting with uveal melanoma were submitted to treatment with protons, with applied dose of 60 GyE in four fractions. According to Cirrone et al.(10), 60% of their patients had T3 lesions(2). The dose levels define the current and intensity of the irradiation beam. Similarly, both parameters were equivalent to those investigated in the proton simulations. According to Table 2, in the simulations with carbon ions one observes that even maintaining a constant beam incidence, the maximum absorbed dose is not directly proportional to the kinetic energy of the incident particle. It varies with the incident kinetic energy of the particle and with the number of particles. In the simulations, a carbon beam with kinetic energy of 840 MeV (70 MeV/u) produced a greater dose deposited per voxel, considering the incidence of 1.0 × 104 carbon ions. Thus, a smaller number of incident carbon ions and current will be necessary to reproduce a therapeutic fraction of 14 GyE, optimizing the utilization of the facilities resources. On their turn, the values regarding maximum deposited doses, number of incident carbon ions and applied current varied by approximately 24%, between maximum and minimum values for each parameter, while the difference between the lowest and highest values of kinetic energy of the incident beam varied by 31%. The depth of the Bragg peak produced by carbon ion beams, as well as by proton beams, depends on the initial energy of the particle in the beam. For carbon ions, the range varied from 11 to 21.5 mm. Such fact is relevant in both situations, as the position of maximum absorbed dose can be adjusted by an external physical parameter independent from the tumor anatomy and biology, but dependent on the kinetic energy of the incident particle. One can say that the physical parameters presented in this study define the operational range of carbon ion therapy in the therapeutic protocols. In the simulations with carbon ion beams, the variation of the kinetic energy of the incident particles was utilized to achieve different depths, while in the simulations with proton beam, an absorbing material was utilized to degrade the beam energy. The processing time in the simulations ranged from 4 hours and 17 minutes to 8 hours, depending on the utilized energy. It is observed that heavy ion radiotherapy planning demands a high computational cost. According to Table 3, the range of the protons beam varies with the thickness of the absorbing material, achieving a variation of 20.5 to 23.0 mm. For the performance of the simulations with proton beams, the thicknesses of the absorbing materials were 6 mm and 8 mm, but, in clinical applications(14) the location and dimensions of the target volume must be considered for a correct configuration of such parameter. Thus, for each clinical case the variation of the absorbing material thickness must be defined for each particle beam entrance position. The maximum deposited doses, maintaining the same number of incident protons and the applied current, varied according to the thickness of the absorbing material. The thicker the absorbing material, the lower the absorbed dose; thus, in order to maintain the recommended dose constant independently from depth, the exposure time must increase with the thickness of the absorbing material. In the presented simulations, the number of processed particles for carbon ions was 100 times smaller than that for protons.The mean values for maximum doses were 1.23 × 10–5 lower for protons in relation to the carbon ion beam, because of the higher value of the carbon ions charge and mass, which, consequently, cause greater ionization in their interaction. Thus, in clinical applications, additional 3 × 105 incident particles and 4 × 104 nA of current are necessary for protons as compared with carbon ion beam. For simulations performed with incident beam energy of 62 MeV/u, the range for carbon ions was 11 mm and, for protons, 23 mm and 20.5 mm, for 6 mm and 8 mm of absorbing material, respectively.One considers that incident energy > 90 MeV/u should be applied for carbon ions to achieve the same depth achieved with 62 MeV/u for protons. CONCLUSION The parameters utilized in the simulations, such as incident kinetic energy of the particles, current, absorbing material, modulator and collimator have aided in the characterization of the absorbed depth dose profile in the eyeball for proton and carbon ion beams. The characterization of such physical parameters is essential in the radiotherapy planning following the geometric distribution of the target volume. The integration of the software tools in different computational environments, involving the Geant4 code and its application libraries, together with the Siscodes, can be useful in the evaluation of ion teletherapy plannings and contribute for future studies approaching dosimetry in carbon ion and proton radiotherapy. The findings of the present study contribute to the development of clinical applications and research in carbon ion and proton radiotherapy. REFERENCES 1. Amaldi U, Kraft G. Radiotherapy with beams of carbon ions. Rep Prog Phys. 2005;68:1861–82. 2. Sobin LH, Wittekind Ch. TNM classification of malignant tumours. 6th ed. New York, NY: Wiley- Liss; 2002. 3. Koyama-Ito H, Kanai T, Minohara S, et al. Carbon ion therapy for ocular melanoma: planning orthogonal two-port treatment. Phys Med Biol. 2007;52:5341–52. 4. Tsuji H, Ishikawa H, Yanagi T, et al. Carbon-ion radiotherapy for locally advanced on unfavorably located choroidal melanoma: a phase I/II dose escalation study. Int J Radiat Oncol Biol Phys. 2007;67:857–62. 5. Tsujii H, Kamada T, Baba M, et al. Clinical advantages of carbon-ion radiotherapy. New J Phys.2008;10. 6. U.S. National Library of Medicine. The visible human project. [cited 2008 Nov 17]. Available from: http://www.nlm.nih.gov/research/visible 7. Trindade BM, Campos TPR. Sistema computacional para dosimetria de nêutrons e fótons baseado em métodos estocásticos aplicado a radioterapia e radiologia. Radiol Bras. 2011;44:109– 16. 8. Mourão AP, Campos TPR. Considerações radiodosimétricas da braquiterapia ocular com iodo- 125 e rutênio/ródio-106. Radiol Bras. 2009;42:43–8. 9. Christóvão MT, Campos TPR. Análise da distribuição espacial de dose absorvida em próton terapia ocular. Radiol Bras. 2010;43:249–54. 10. Cirrone P, Cuttone G, Di Rosa F, et al. The hadrontherapy Geant4 advanced example. In: 4th Workshop on Geant4 Bio-medical Developments, Geant4 Physics Validation. 2005 July 13–20; Genova, Italy. 11. National Council on Radiation Protection and Measurements. Report No. 144 – Radiation Protection for Particle Accelerator Facilities. Bethesda, MD: National Council on Radiation Protection and Measurements; 2003. 12. Ondreka D, Weinrich U. The Heidelberg ion therapy (HIT) accelerator coming into operation. Proceedings of EPAC08:979–81; Genoa, Italy. 13. Endo K, Fang Z, Fukumoto S, et al. Compact proton and carbon ion synchrotrons for radiation therapy. Proceedings of EPAC 2002:2733–5; Paris, France. 14. Cirrone GAP, Cuttone G, Lojacono RA, et al. A 62-MeV proton beam for the treatment of ocular melanoma at Laboratori Nazionali del Sud-INFN. IEEE Transactions on Nuclear Science. 2004;51:860–5. 15. Greco C, Wolden S. Current status of radiotherapy with proton and light ion beams. Cancer. 2007;109:1227–38. 1. PhD, Technologist at Centro de Desenvolvimento da Tecnologia Nuclear (CDTN), Belo Horizonte, MG, Brazil. 2. PhD, Professor, Department of Nuclear Engineering, Universidade Federal de Minas Gerais (UFMG), Belo Horizonte, MG, Brazil. 3. Post-Doctorate, Department of Nuclear Engineering, Universidade Federal de Minas Gerais (UFMG), Belo Horizonte, MG, Brazil. Mailing Address: Marília Tavares Christóvão. Avenida Presidente Antônio Carlos, 6627, Campus da UFMG, Pampulha, Caixa Postal 941 Belo Horizonte, MG, Brazil, 31270-901. E-mail: marilia@cdtn.br Received November 16, 2010. Accepted after revision October 25, 2011. * Study developed at Department of Nuclear Engineering, Universidade Federal de Minas Gerais (UFMG), Belo Horizonte, MG, Brazil. |
|
Av. Paulista, 37 - 7° andar - Conj. 71 - CEP 01311-902 - São Paulo - SP - Brazil - Phone: (11) 3372-4544 - Fax: (11) 3372-4554