INTRODUCTION
In diagnostic mammography, different calculation methods and phantoms are used to estimate glandular dose. Each method and/or model has an intrinsic set of conversion factors that relate the kerma or the skin entrance exposure to the absorbed dose in the breast or glandular tissue. A method proposed by Wu et al.(1) and utilized worldwide is based on the normalized glandular dose (D
gN). Such conversion factor relates the kerma, measured at a reference position, with the dose on the mammary gland.
Different authors have published conversion factors applied to dosimetry in mammography(2–4). However, dosimetric methods are significantly dependent upon the characteristics of utilized models and equipment (geometry, materials composition and radiographic technique)(1,5,6).
The present study is aimed at reviewing data from dosimetric studies in computational simulations and discussing their limitations regarding their utilization in dosimetry for constancy tests and actual breast dosimetry. Different models recommended by the International Commission on Radiation Units and Measurements (ICRU) (ICRU Report 48)(7) commonly utilized in hospitals and clinics(8) were considered in the study.
In order to appropriately understand the objectives of the present study, it is important to define what performance and constancy tests as well as actual dosimetry in mammography are. Performance tests are defined as a set of measurements and analysis to confirm compliance with minimum performance standards. According to the Government Order 453 of Agência Nacional de Vigilância Sanitária (Anvisa) (Brazilian Agency of Health Surveillance)(9), constancy tests are routine evaluations of technical and performance parameters for instruments and equipment, and the study of the behavior of such parameters as a function of time. On the other hand, actual dosimetry is the determination of absorbed dose to organs or tissues under study in a specific case for a specific patient. In other words, it means the determination of the dose considering the particularities of each patient (anatomy and procedures utilized) in order to figure dose values as closely as possible to those absorbed by specific organs in a procedure. Actual and individualized dosimetry has increasingly become a more widely known and utilized practice(4,5,10,11). The analysis of dose in mammography can be defined as the constancy test or actual dosimetry in a radiosensitive organ, depending upon the way it is performed and the application of gathered data. The Government Order 453 from Anvisa(9) defines “absorbed dose” as the “quantity expressed by
D = dE/dm, where
dE is the expected value of energy deposited by radiation in an elementary volume of mass
dm. The unit of absorbed dose in the International System (IS) is joule per kilogram, denominated gray (Gy)”. The dose evaluations, performed according to the recommendations of quality control tests in mammography(9,12), provide a comparative basis of the equipment performance in similar boundary conditions, i.e., constancy tests.
In the present study, the behavior of dosimetric quantities simulated by means of computational tools for different models was evaluated considering two forms of dosimetry application: constancy tests and actual dosimetry.
MATERIALS AND METHODS
The Monte Carlo Geant4 code (version 8.2.p01) was utilized to simulate the radiation transport. The calculations were performed maintaining the irradiation beam geometry constant, alternating the incident radiation spectrum and the breast phantom. Absorbed dose, photon fluence and kerma data were collected.
The irradiation geometry was computationally generated considering a spherical volume with a 0.8 m radius, filled with dry air, according to the ICRU definitions (ICRU Report 44)(13). The bucky dimensions are (18.0 Χ 24.0 Χ 0.2) cm3, with the source-bucky distance corresponding to 61.9 cm, according to the specifications of the Lorad MIII equipment(14). A polymethylmethacrylate (PMMA) compressor measuring (18.0 Χ 24.0 Χ 0.2) cm3 was simulated over the breast model.
The different breast phantoms were simulated in this geometry, each one containing three sensitive volumes at different depths: entrance, middle and exit of the model. Each sensitive volume with (1.0 Χ 1.0 Χ 0.1) cm
3 was defined to collect the absorbed dose and the photon fluence at the depth of interest. An air volume similar to a free-in-air ionization chamber, with a sensitive volume of 6.0 cm
3 was simulated over the model and below the PMMA compressor. The reference kerma value collected in the simulated ionization chamber (kermaIC) – utilized for data normalization was simulated in the ionization chamber positioned at a 4.0 cm-height and below the compressor without the presence of the breast phantoms, i.e., it does not take into account for the backscattering caused by the models. A poit source, located at the level of the focal point, with an irradiation field with the same dimension of the bucky entrance (18 Χ 24) cm
2, simulated spectra between the accelerating voltages of 26 to 34 kVp for the Mo-Mo and Mo-Rh target-filter combinations. Table 1 lists all the simulated spectra and their respective half-value layers (HVL), without the presence of the compressor.
Six homogeneous, non-anthropomorphic breast models, were simulated as representative of a standard breast, defined by a 50% fat and 50% glandular tissue composition(7): four non-anthropomorphic models proposed by ICRU(7) – idealized by Dance, NA type 76-001, RMI type 156 and Barts –, one model for dosimetry proposed by Keithley Instruments and one model produced in Brazil (PhantomMama)(15). All the homogeneous, non-anthropomorphic models were compared with an anthropomorphic breast voxel phantom(16), with a description of glandular tissue in the medial region. The simulated voxel model representing a medium sized breast with 4.1 cm thickness when compressed, was based on an actual breast images acquired by magnetic resonance imaging, and has (1.38 Χ 1.38 Χ 1.00) mm
3 voxels. All the seven models, with their respective internal structures (if applicable), are shown on Figure 1.

Figure 1. Schematic image of simulated non-anthropomorphic models and anthropomorphic breast model.
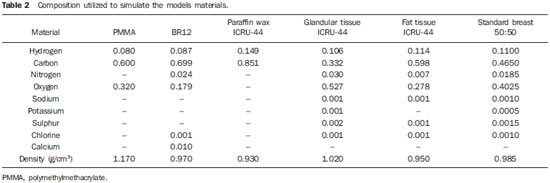
The models proposed by Barts and Keithley were simulated with a type BR12 epoxy composition; the model proposed by Dance was composed of a mixture of material simulating fat and glandular tissues and the remaining models were based on the PMMA material with internal volumes composed of paraffin wax. The composition of materials utilized in the models description can be observed on Table 2. The internal objects that allow the control of mammographic image quality were not simulated.
In the simulations, data were collected for the calculation of the following values: kerma, absorbed dose absorbed in organs or tissues representative of the mammary gland or in the breast as a whole, and the photon fluence crossing the sensitive collection volumes in the model. Such values allowed the evaluation of the conversion factor D
gN by means of the division of the absorbed dose by the glandular tissue (D
g) or the absorbed dose by the model (D), and the kerma
IC.
It is important to highlight that some models do not allow the tissues differentiation and, consequently, do not allow the determination of D
g, as such models are composed of homogeneous mix of simulated material. In this case, D ends up being equivalent to D
g. In the present study, the authors considered the kerma collected without backscattering in a chamber positioned at 4.0 cm above the bucky. Such approximation is valid, as the models presented a thickness close to 4.0 cm.
Additionally, in order to facilitate the comparison of data, the authors utilized the absorbed dose in the model by photons emitted by the source (D), in mGy, which represents the probability of energy absorption by mass unit per photon emitted from the source. In order to convert such value into dose in the models by load collected in the tube, it was necessary to multiply the D values by the number of photons emitted by mAs per unit of irradiated area. In this case the area corresponded to 432 cm
2.
RESULTS
The data presented compare dosimetric quantities utilized in constancy tests and in patients dosimetry, in the latter case focusing on some parameters that involve dosimetry in anthropomorphic breast voxel model. For such analysis, the following parameters were utilized: D
gN, kerma
IC, glandular dose, or absorbed dose in an equivalent material, absorbed dose in the breast or in the model, and absorbed dose at different depths of the model. Additionally the photons fluence and the HVL of the collected fluence were also evaluated.
Figure 2 shows the comparative results for D
gN for all the studied models. All of them present a similar behavior with a tendency towards D
gN increase as the HVL increases.

Figure 2. Behavior of D
gN as a function of HVL for the different studied models.
The point of apparent DgN decrease marks the alteration of the combination Mo-Mo target-filter at the 0.293 and 0.304 points, and for Mo-Rh, at the 0.300 point, demonstrating the influence of the spectrum generated by different target-filter compositions on D
gN. As compared with the breast voxel model, the models proposed by Dance, Keithley and Barts presented greater similarity in the D
gN curve format as a function of HVL. However, the models defined as Keithley and Barts overestimated the value of D
gN. The model proposed by Dance underestimated the values of D
gN, with the smallest variations from point to point, as compared with the voxel model. In spite of the fact that the model NA type 76-001 presented smaller variations in the values of D
gN, the curve shape was not constant, with underestimation and overestimation points as compared with the voxel model. The conversion of kerma into glandular dose by means of the D
gN factor is dependent upon the measurements of kerma
IC, either with or without backscattering, and upon the collection geometry (over the model and beside the model). Thus, it is important to discuss the values of kerma
CI defined in each simulation condition.
The chart presented on Figure 3 shows the behavior of simulated kermaIC without considering backscattering. As expected, for each target-filter combination, the kerma in the chamber demonstrated a decreasing behavior with the increase of HVL. The general characteristic of the models simulated will be represented by means of the addition of the backscattering factor and the conversion factor of kermaIC into glandular dose.
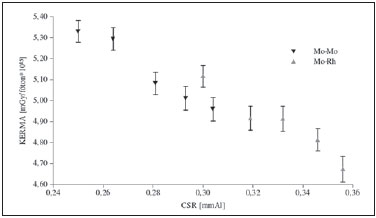
Figure 3. Chart showing the behavior of kerma by photons emitted by the source to the chamber at 4 cm above the bucky.
It is important to know the dose in the model or in the breast in order to compare the models (Figure 4A) and the dose in the glandular tissue or equivalent material (Figure 4B).
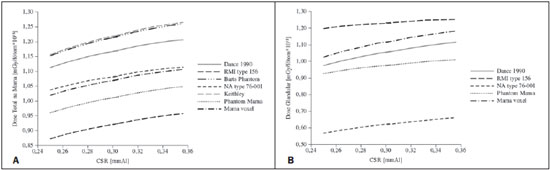
Figure 4. Chart showing the behavior of dose normalized by photons emitted by the source on the breast or model (A) and dose on the gland or equivalent material (B) for the studied models and spectrum.
The charts on Figure 4 demonstrate a tendency of increase in the probability of energy deposition energy as a function of the increase in HVL. The probability of total absorbed dose in the breast (Figure 4A) presented a more enhanced increase than the probability of glandular dose absorption. As regards the probability of total dose absorbed in the breast, the simulator NA type 76-001 presented the smallest variations in comparison with the voxel model, and the RMI type 156 presented the largest variation. The probability of glandular absorbed dose in the simulator defined by Dance in 1990 presented the smallest variations in comparison to the voxel model. The NA type 76-001 presented the greatest variation. For the studied spectra, considering the dose of greater interest in radiological protection (glandular dose), the behavior of the model proposed by Dance in 1990 was most similar to the behavior of the voxel model.
Figure 5 shows the behavior of absorbed dose in the sensitive volumes as the radiation beam penetrates the models. In general, for the same models and entrance spectrum, the absorbed dose decreases with the beam penetration depth.
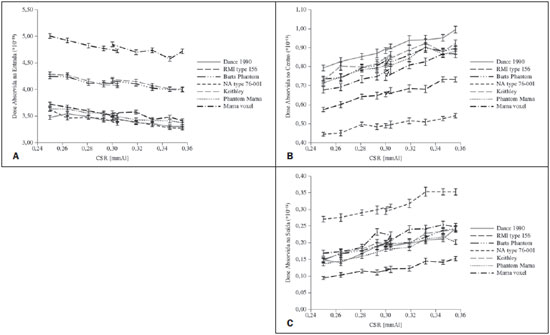
Figure 5. Behavior of dose by normalized photons emitted by the source on the entrance (A), medial (B) and exit (C) volumes of the studied models for all simulated spectra.
The authors observed the absorbed dose tendency to decrease in the entrance volume as the incident beam HVL increases. In this collection, all the non-anthropomorphic models presented doses lower than the one calculated for the voxel model. The Keithley and the Barts models were the ones presenting the absorbed dose values in the entrance volume closer to those in the breast voxel model.
The sensitive volumes recorded the photon fluence, allowing the evaluation of changes in the quality of the radiation beam as it penetrated the simulated models. The spectrum collected by each sensitive volume showed that the HVL values generally present variations of > 70% in the comparison between entrance and exit sensitive volumes, for the same model and radiographic technique. In the comparison of the entrance HVL values amongst all the models, a variation of < 10% was observed. As the values of entrance volumes HVL variation, the Barts model presented greater proximity to the values calculated for the voxel model. On the other hand, for the HVLs calculated for the medial and exit sensitive volumes, the RMI type 156 model presented the closest values to the ones calculated for the sensitive volumes simulated in the voxel model. As regards the models with the greatest HVL variations, the RMI type 156, NA type 76-001 and PhantomMama presented the greatest variations for the entrance volume, while the Barts, NA type 76-001 and Keithley models presented the greatest variations in the medial volume and the Barts model presented the greatest variation in the exit volume.
DISCUSSION
In all the models, the energy absorption decreases as a function of beam penetration. However this occurs in a differentiated manner because of the incident beam radiation scattering processes and photon absorption, which is dependent upon the photons energy and model material. The alterations observed in the dose are compatible with changes in the quality of the beam estimated by HVL. In general, the Barts and Keithley models presented the smallest variations in absorbed dose normalized by photon emitted by the source, so they compare to the voxel model, for all sensitive volumes and all studied spectra. Variations of 10% to 15% in the HVL were calculated for the entrance volumes, 0% to 10% for the medial volumes and 0% to 18%, for the exit volumes. On the other hand, the NA type 76-001 model presented the greatest HVL variations in all the studied spectra. Variations between 14% and 28% were calculated for the entrance volumes, 34% and 41% for the medial volumes, and 32 and 61% for the exit volumes.
As expected, the data regarding absorbed dose normalized by the number of photons emitted by the source confirmed that the absorbed dose in the breast and the absorbed dose in the gland were different. Thus, as the interest is actual dosimetry in the patient, it is important to utilize models with anthropomorphic geometry, tissue composition and location of glandular tissue similar to those of the patient of interest. On the other hand, for the activity of dosimetry for assessment of constancy of the X-radiation emitting equipment, one should maintain the data collection process and the model constant during the performance of the tests.
The present study demonstrated some of the geometrical limitations of the non-anthropomorphic models as compared with the anthropomorphic model. It was demonstrated that the choice for the non-anthropomorphic model depends upon the quantity to be measured or simulated. In other words, if interest lies in the evaluation of D
gN and D
g values for median breasts with glandular tissue in the medial region, the model proposed by Dance is recommended. If the quantity of interest is the total absorbed dose in the breast, the most recommended model is the NA type 76-001, among the studied ones.
Taking the issues related to radiological protection in mammography into consideration, the model proposed by Dance is recommended that as presenting a behavior similar to the voxel model representative of a median breast, even if one considers that such model underestimates all values calculated for D
gN. In articles published in 2005, Zankl et al.(4) and Dance et al.(5,11) demonstrated the existing differences based on the variations in the spatial distribution of the breast tissue. The recent article published by Nigapruke et al.(17) discloses results similar to those in the present study as regards the behavior of normalized dose as a function of incident spectrum energy and deposited dose as a function of depth.
The present study does not question the use of non-anthropomorphic models for constancy tests. Actually, considering that this is a performance test, variations in the radiographic imaging system will be perceived provided the data collection geometry, the model and the radiographic technique remain the same throughout the test. However, it is the utilization of such models in the relationship with actual dosimetry in patients that is questionable, and different parameters should be considered(5). In cases where the interest lies in calculating the glandular dose in actual breasts, the current most recommended procedure is to perform the measurement of the breast entrance air kerma, utilizing conversion factors to correlate such measurement with breast absorbed dose. For appropriate conversion of the values, it is necessary to consider the anatomic characteristics of the breast, its compressed thickness and the characteristics of the X-ray beam emitted by the equipment: target-filter combination and HVL.
CONCLUSIONS
The authors observed that mathematical model recommended for estimating the actual dose, utilizing conversion factors of skin entrance air kerma into glandular dose, depends upon characteristics such as equipment geometry, particularities of the breast anatomy and adopted radiographic technique. Such conversion factors must be carefully selected according to the characteristics of the imaging system and the anatomy of the breast of interest. However the authors could observe that non-anthropomorphic models may be utilized to indicate constancy parameters of the mammographic imaging system, but such models do not represent the glandular dose in actual breasts. Thus, as dosimetric quantities are calculated, it is important to select the model with greatest similarity to the breast of interest, so that the applied correction factors are appropriate.
Based on these data, the authors suggests the determination of correction factors and/or coefficients, the HVL of the spectra utilized in mammography, considering other target-filter combinations and maximum accelerating voltages to assist in the calculation of actual DgN for different configurations of equipment currently in the market. Additionally, the authors suggests the study of “voxelized” models for the generation of actual glandular dose, i.e., the idealization of an actual model that comes closer to the distribution of an anthropomorphic breast for use in the estimation of actual dose in the breast.
REFERENCES
1. Wu X, Gingold EL, Barnes GT, et al. Normalized average glandular dose in molybdenum target-rhodium filter and rhodium target-rhodium filter mammography. Radiology. 1994;193:83–9.
2. Dance DR. Monte Carlo calculation of conversion factors for the estimation of mean glandular breast dose. Phys Med Biol. 1990;35:1211–9.
3. Wambersie A, DeLuca PM, Zoetelief J. Appendix E: Review of Monte Carlo calculations for assessment of mean glandular dose in mammography. Journal of the ICRU. 2005;5:93–9.
4. Zankl M, Fill U, Hoeschen C, et al. Average glandular dose conversion coefficients for segmented breast voxel models. Radiat Prot Dosimetry. 2005;114:410–4.
5. Dance DR, Young KC, van Engen RE. Further factors for the estimation of mean glandular dose using the United Kingdom, European and IAEA breast dosimetry protocols. Phys Med Biol. 2009;54:4361–72.
6. Oliveira ML, Maia AF, Nascimento NCES, et al. Influência da dependência energética de dosímetros termoluminescentes na medida da dose na entrada da pele em procedimentos radiográficos. Radiol Bras. 2010;43:113–8.
7. International Commission on Radiation Units and Measurements. Phantoms and models in therapy, diagnosis and protection. ICRU Report 48. Bethesda, MD: ICRU; 1992.
8. Hoff G, Almeida CEV, Drexler GG. Estimating conversion coefficient of KERMA free in air to glandular dose in mammography: a comparison between BR12 model and a realistic voxel model. In: IEEE Transactions on Nuclear Science (TNS), NSS e MIC, 2006, San Diego, CA, USA.
9. Brasil. Ministério da Saúde. Agência Nacional de Vigilância Sanitária. Diretrizes de proteção radiológica em radiodiagnóstico médico e odontológico. Portaria nº 453, de 1º de junho de 1998. Brasília, DF: Diário Oficial da União, 2/6/1998.
10. Oliveira M, Nogueira MS, Guedes E, et al. Average glandular dose and phantom image quality in mammography. Nuclear Instruments and Methods in Physics Research – Section A. 2007;580: 574–4.
11. Dance DR, Hunt RA, Bakic PR, et al. Breast dosimetry using high-resolution voxel phantoms. Radiat Prot Dosimetry. 2005;114:359–63.
12. Brasil. Ministério da Saúde. Agência Nacional de Vigilância Sanitária. Radiodiagnóstico médico: desempenho de equipamentos e segurança. Brasília, DF: Ministério da Saúde; 2005.
13. International Commission on Radiation Units and Measurements. Tissue substitutes in radiation dosimetry and measurement. ICRU Report 44. Bethesda, MD: ICRU; 1989.
14. Hoff G. Cálculo da dose em glândula mamária, utilizando o código de transporte de Monte Carlo MCNP, para as energias utilizadas em mamografia [Tese de Doutorado]. Rio de Janeiro, RJ: Universidade do Estado do Rio de Janeiro; 2005.
15. Peixoto JE. Manual de instruções para as medidas de controle de qualidade dos parâmetros técnicos da mamografia. MRA. [acessado em 19 de agosto de 2010]. Disponível em: http://mra.com.br/prod_mra_cqpm.html
16. Hoff G, Cassola VF, Anés M, et al. Construção de simuladores de mama do tipo voxel, através de imagens tomográficas. Anais do VIII Congresso Brasileiro de Física Médica. 2003;I:232–5.
17. Nigapruke K, Puwanich P, Phaisangittisakul N, et al. Monte Carlo simulation of average glandular dose and an investigation of influencing factors. J Radiat Res (Tokyo). 2010;51:441–8.
1. Master, Fellow PhD degree, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) / Universidade Federal de Pernambuco (UFPE) / Departamento de Energia Nuclear (DEN), Recife, PE, Brazil.
2. PhD, Professor TI 40, Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS) / Grupo de Experimentação e Simulação Computacional em Física Médica (GESiC), Porto Alegre, RS, Brazil.
Mailing Address:
Gabriela Hoff
Avenida Ipiranga, 6681, prédio 10, sala 207, Partenon
Porto Alegre, RS, Brazil, 90619-900
E-mail: ghoff.gesic@gmail.com
Received August 3, 2010.
Accepted after revision October 19, 2010.
* Study developed at Pontifícia Universidade Católica do Rio Grande do Sul (PUCRS) / Grupo de Experimentação e Simulação Computacional em Física Médica (GESiC), Porto Alegre, RS, Brazil.
 Vol. 43 nº 6 - Nov. / Dec. of 2010
Vol. 43 nº 6 - Nov. / Dec. of 2010